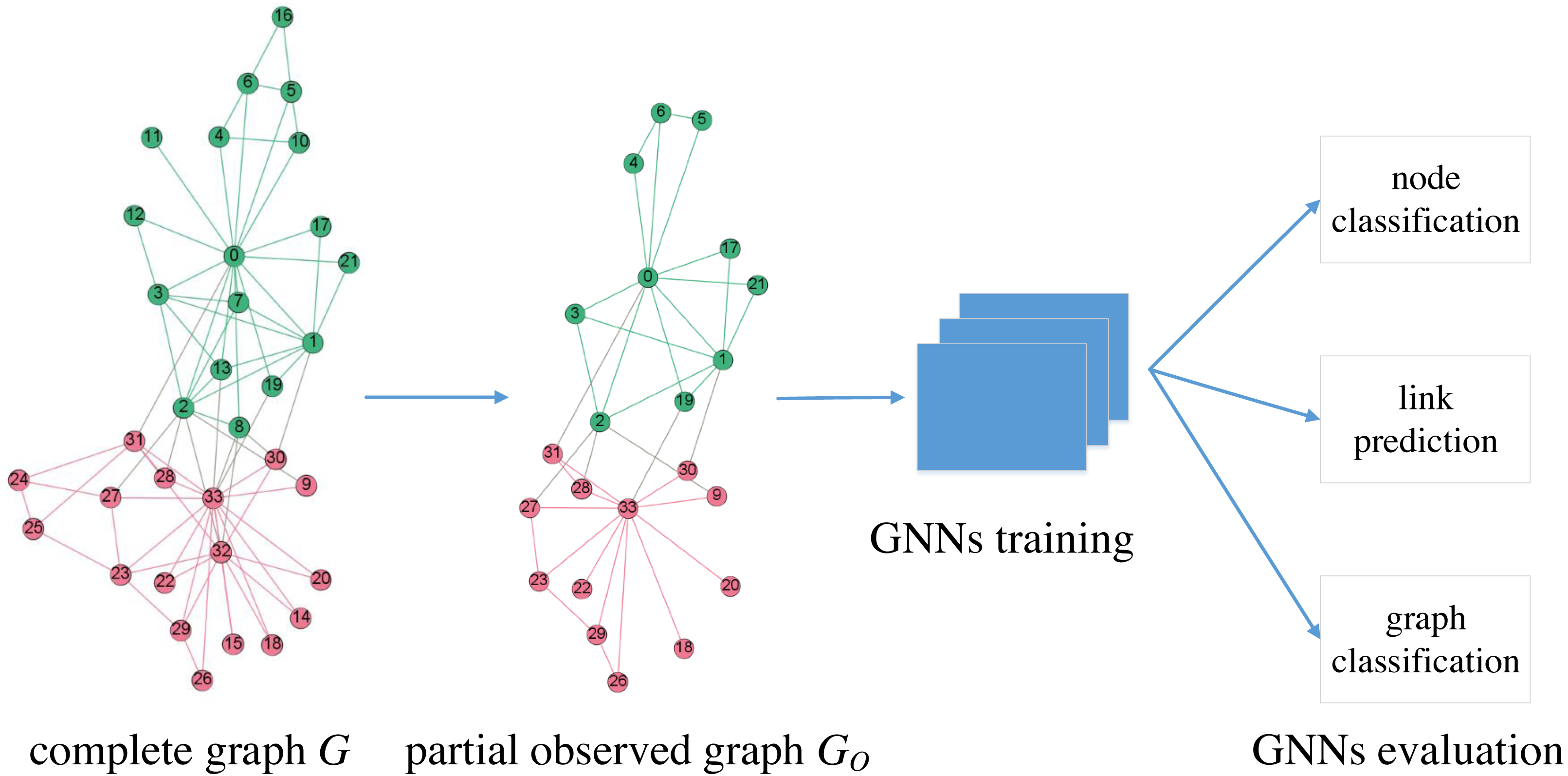
본 포스트에서는 Graph Neural Network에 대한 배경과 MNIST SuperPixel에 대한 응용, 그리고 STGNN에 대해 소개하고자 합니다.
What is Graph Neural Network(GNN)?
그래프는 node 혹은 vertex라 불리는 점과, 이를 연결하는 link 혹은 edge라 불리는 선으로 구성된 자료 구조입니다. Node간의 연결 구조를 인접행렬 (adjacency matrix)로 표현하며, 각 구성요소들인 node와 link의 정보는 node feature matrix, link feature matrix 등으로 표현할 수 있습니다.
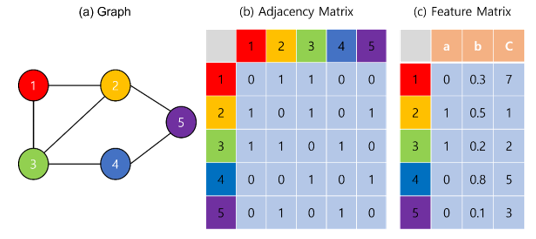
GNN은 adjacency matrix와 feature matrix를 사용하여, 그래프 구조를 조금 더 쉽게 처리할 수 있는 인공 신경망입니다.
Category of GNN
이번 절에서는 ‘A Comprehensive Survey on Graph Neural Networks’ 논문 의 내용을 바탕으로 GNN의 분류를 말씀드리고자 합니다. GNN은 크게 RecGNN (Recurrent GNN)과 ConvGNN (Convolutional GNN)으로 나뉘고 ConvGNN은 다시 한번 Spectral-based ConvGNN과 Spatial-based ConvGNN으로 나뉩니다. 각각 GNN의 대표적인 모델과 함께 벤 다이어그램으로 표현하면 다음과 같습니다. GCN 은 Spectral ConvGNN의 근사형태로 볼 수 있으며 동시에 Spatial ConvGNN으로도 해석할 수 있어, 둘 사이의 중간 연결다리의 역할을 합니다.
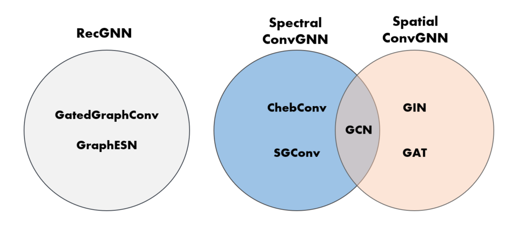
Recurrent GNN
RecGNN은 GNN의 가장 초창기 형태입니다. Node의 hidden feature는 이웃 node들의 feature 및 link의 feature로부터 recurrent하게 stable equilibrium에 도달할 때까지 계산됩니다. 하지만 현재는 equilibrium point의 불안정성, 그리고 BPTT(Back-Propagation Through Time)의 계산 복잡도 때문에 현재는 잘 쓰이지 않는 형태입니다.
현재 node의 feature를 이웃한 node의 feature로부터 업데이트 하는 방식은 message passing이라는 개념으로 해석할 수 있습니다. 이는 후에 spatial-based ConvGNN을 이해할 수 있는 좋은 framework가 되기에, 자세한 설명은 해당 절에서 하도록 하겠습니다.
Spectral-based Convolutional GNN
Spectral-based ConvGNN은 normalized laplacian matrix $L≡I-D^{-1/2} AD^{-1/2}$의 eigen vector들을 basis로 하는 graph fourier space에서 연산을 진행합니다. 이때 D는 degree matrix입니다. 이는 graph signal theory를 기반으로 하여 발전하였고, 일반적으로 다음과 같은 식으로 node의 상태를 update합니다.
\[x^{'}= Ug_\theta U^T x\]위 식에서 U는 eigen vector들로 이루어진 fourier transform matrix이며 $g_θ$는 trainable parameter θ로 이루어진 함수입니다. U를 구하는데 계산 복잡도가 크기 때문에, 이를 어떻게 근사하는지, g_θ의 형태를 어떻게 하는지에 따라 ChebConv , ARMAConv , SGConv 등의 다양한 model들이 제안되었습니다. Spectral-based ConvGNN의 장점은 고정된 구조의 그래프의 경우에는 graph-wise feature를 쉽게 추출할 수 있지만, 구조가 달라지는 데이터셋에 대해서는 fourier transform matrix U가 달라지기 때문에 잘 적용되지 않습니다. 또한 그래프에 방향성이 있는 directional graph의 경우, laplacian matrix가 symmetric하지 않기 때문에, 적용하기 어렵습니다.
Spatial-based Convolutional GNN
Spatial-based ConvGNN은 adjacency matrix만을 사용하여 node의 feature를 업데이트합니다. 이를 message passing이라는 개념을 도입하여 해석할 수 있는데, 이는 아래와 같은 식으로 표현됩니다.
\[x_i^{'}=γ_\theta (x_i,\sum_{j∈N(i)} ϕ_Θ (x_i,x_j,e_ij ))\]- Node feature $x_i$, $x_j$ 와 link feature $e_{ij}$를 input으로 가지는 message function $ϕ_Θ$를 통해 message를 계산합니다.
- 모든 이웃한 node에서 만들어진 message들을 sum/mean/max 등의 permutation-invariant한 aggregation function으로 합칩니다.
- 2번의 결과, 합쳐진 message들과 node feature $x_i$를 input으로 가지는 update function $γ_Θ$ 를 통해 다음 node의 feature를 계산합니다.
Spatial-based ConvGNN은 각 단계의 message function $ϕ_Θ$, aggregation function ∑, update function $γ_Θ$ 의 형태에 따라 GAT , GIN 등의 종류로 나뉘어집니다. Spatial-based ConvGNN은 인접행렬만을 이용하기 때문에 fourier transform matrix를 계산해야하는 spectral-based ConvGNN에 비해 계산 복잡도가 작고, 구조가 다른 그래프들을 다루는 데이터 셋들이나 adjacency matrix가 asymmetric한, 방향성이 있는 그래프에 잘 적용된다는 장점이 있습니다.
Application
상술된 RecGNN과 ConvGNN을 사용할 수 있는 가장 단순한 application에는 node (혹은 link, graph) classification 및 regression이 있을 것입니다. 하지만 이와는 결이 다른 두가지의 큰 분야가 연구되고 있습니다. 그 첫번째는 GAE(Graph Auto Encoder) 입니다. 일반적인 auto encoder와 같이, encoder와 decoder로 이루어진 그래프 생성 모델로서 input graph와 유사한 graph를 generation하고, graph를 vector로 embedding 하는 것을 목표로 하는 분야입니다. 두번째로 STGNN(Spatial-Temporal GNN)은 multi-variable time series data를 다루는데 쓰입니다. 이는 본 포스팅 글 아래에서 좀 더 자세하게 살펴볼 예정입니다.
MNIST SuperPixel
GNN을 활용한 다양한 task 가운데, 가장 기초적인 task로서 MNIST SuperPixel에 대한 label classification을 진행하였습니다. 우리가 흔히 알고 있는 MNIST 데이터셋은 28 * 28의 픽셀로 구성된 0부터 9 사이의 숫자 이미지 데이터셋입니다. 이미지 데이터의 처리 및 해석을 위한 다양한 영상 분할 방법이 존재하며, 이 중 Super pixel을 적용한다면, graph의 형태로 변환하기 용이해 GNN을 사용한 classification을 할 수 있습니다. Super pixel은 공통적인 특징을 가진 pixel들을 그룹화한 데이터입니다. 이를 위한 방법으로 그래프 기반 방법이나, 기울기 기반 방법 등을 사용할 수 있습니다. 다양한 알고리즘 가운데 가장 최근에 나온 SLIC 알고리즘 의 경우에는 5차원 공간 (2D 위치 및 3D RGB)에서 KNN-clustering을 통해 경계를 나누게 됩니다.

Super pixel 이미지를 K-Nearest Neighbor Graph 알고리즘을 통해 인접한 k개의 super pixel들을 연결함으로써 graph 형태의 데이터로 변환할 수 있습니다. 여기서 사용한 데이터셋은 MONET 의 저자들인 publish한 것으로, 그래프의 adjacency matrix와 노드로 취급되는 super pixel의 gray-scale color 및 2D position으로 구성되어 있습니다.

Graph Classification
GNN을 이용한 MNIST label classification의 process는 아래과 같습니다.
- MNIST SuperPixel 데이터로부터 adjacency matrix와 node feature(gray color)을 가져온다.
- GNN layer를 사용하여 node의 정보가 embedding된 hidden feature를 계산한다.
- Hidden node feature로부터 pooling을 통해, graph embedding을 구한다.
- MLP을 통해 라벨 분류에 필요한 feature를 추출한다.
- 추출된 feature에 softmax 혹은 sigmoid function등을 적용 각 라벨에 대한 확률을 구한다.
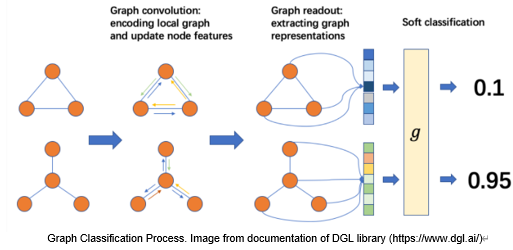
Result
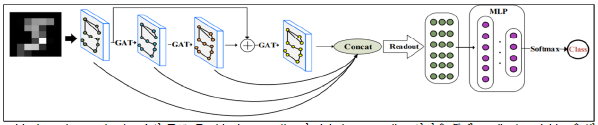
Hierarchical Graph Neural Network 구조 에 대해 GCN, ChebConv, GAT를 사용하여 딥러닝 모델을 구성하였습니다.
| Model | GCN | ChebNet | GAT |
|---|---|---|---|
| Accuracy | 0.73 | 0.89 | 0.85 |
| Cross Entropy Loss | 1.767 | 1.574 | 1.64 |
| # Parameters | 30,090 | 42,442 | 464,394 |
| Embedding Size | 64 | 64 | 64 |
| Hop Length | - | 5 | - |
| Multi-Head | - | - | 4 |
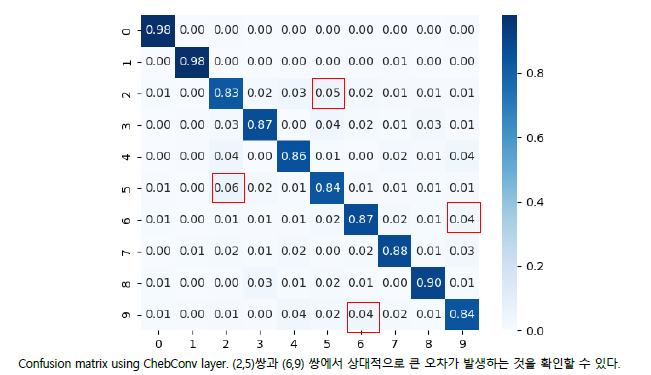
여러 실험을 통해 ChebConv으로 구현한 모델에서 가장 성능이 우수하다는 것을 확인할 수 있었습니다. 이 외에도, Confusion matrix를 통해 잘못된 라벨을 예측한 퍼센트를 확인해본 결과, (2,5), (6,9)와 같이 rotation, flip 했을 때 구분할 수 없는 이미지들에 대해서 상대적으로 오차가 큰 것을 확인할 수 있었습니다.
Spatial-Temporal Graph Neural Network (STGNN)
Multi-variable time series data는 여러 개의 변수들이 상호작용하며 시간에 따라 변화하는 데이터들을 통칭합니다. 매우 다양한 분야에서 이러한 종류의 데이터를 관찰할 수 있는데, 대표적으로 사람의 움직임에 따른 팔꿈치와 손의 위치 등의 변화가 있습니다. 뿐만 아니라 교통망 데이터, 뉴런의 활동 데이터들 역시도 이러한 multi-variable time series data의 한 종류라고 할 수 있습니다.
Spatial-Temporal GNN은 이러한 데이터들을 분석하기 위해 제시된 인공신경망 구조입니다. 데이터에 따라 변수들 간의 상관관계는 알려지지 않을 수도 있으며 (ex. stock market data), 반대로 주어져 있을 수도 있습니다 (ex. traffic data). 즉, STGNN은 데이터에 따른 상관관계를 graph로서 inference 해야 하는 경우도 있습니다. 이렇게 만들어진 그래프를 기반으로, 변수의 시계열 패턴과 다른 변수 들로부터의 영향을 고려하여 multi-variable time series prediction을 합니다.
이 절에서는 STGNN의 모델 중 대표적으로 아래와 같은 구조를 가지는 MTGNN 을 소개해 드리겠습니다.
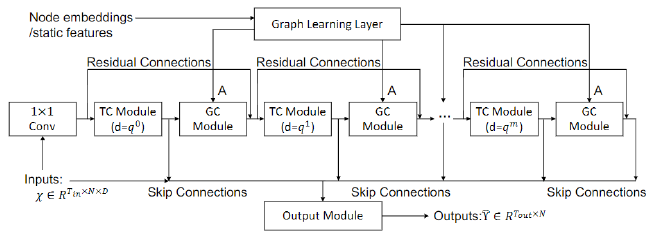
만약 주어진 graph data가 없다면, 우선 graph learning layer를 통해 weighted directed graph를 inference합니다. 각 노드 쌍 $i$,$j$에 대하여, 이를 연결하는 link의 weight는 다음과 같은 식으로 계산됩니다. 이때 $M_i$,$M_j$는 각 노드의 embedding입니다.
\[ReLU(tanh tanh (α(M_i M_j^T-M_j M_i^T) )\]구성된 graph를 기반으로 Temporal Convolution Module과 Graph Convolution Module을 반복해 거치면서 변수들 간의 spatial한 상호작용과 time-dependent한 성질을 반영합니다.
Temporal convolution은 receptive field의 크기를 다르게 하여 다양한 scale의 temporal(time) effect를 고려할 수 있는 inception layer 를 기반으로 구성됩니다. 또한 computational cost를 낮추고 넓은 window를 볼 수 있는 dilation technique 를 사용하였습니다.
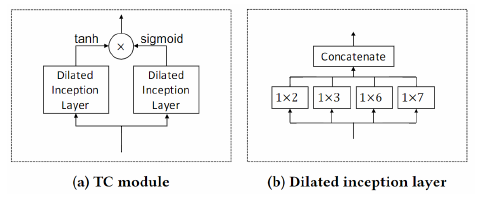
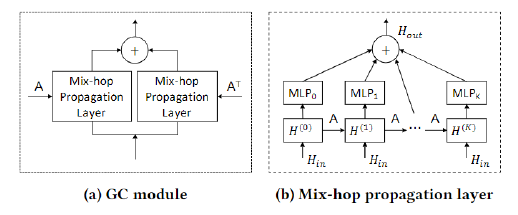
Graph convolution의 경우, inception layer와 비슷한 개념을 공유하는 mix-hop layer 를 사용하였습니다. 이를 통해 한 노드로부터 다양한 거리(hop length)에 있는 노드들의 spatial한 영향을 고려할 수 있습니다.
마치며…
이렇게 GNN의 각 layer에 대한 간략한 소개와 이를 사용한 MNIST classification, 그리고 multi-variable time series data에 적용할 수 있는 STGNN에 대한 글을 작성해 보았습니다. 혹시 궁금한 내용이 있으시다면 댓글로 달아 주시면 답변해 드리겠습니다.